正弦型函数是数学中的重要概念，广泛应用于各个领域，本文旨在深度解析正弦型函数的性质、图像特征，并探索其在实践中的应用，通过专题研究，帮助读者更好地理解和掌握正弦型函数。

正弦型函数基础知识

正弦型函数一般形式为 y = A sin(ωx + φ)，其中A、ω、φ为常数，A代表振幅，决定函数的波动范围；ω代表频率，决定函数的周期；φ代表初相，决定函数图像的起始位置。

正弦型函数具有以下基本性质：

1、周期性：正弦型函数具有周期性，周期为 T = 2π/ω。

2、奇偶性：当φ=0时，函数为奇函数；当φ=π/2时，函数为偶函数。

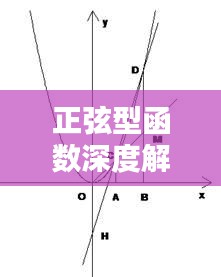
3、图像特征：正弦型函数的图像是一条在x轴上起伏变化的曲线，形状和振幅、频率、初相有关。

正弦型函数的图像与性质分析

正弦型函数的图像分析主要包括图像变换和图像特征描述，通过图像变换，可以直观地展示振幅、频率、初相等参数对函数图像的影响，通过对图像特征的分析，可以进一步理解正弦型函数的性质。

正弦型函数的应用探索

正弦型函数在各个领域有广泛的应用，在物理学中，正弦型函数用于描述振动、波动等现象；在工程学领域，正弦型函数用于信号处理、交流电路分析；在经济学领域，正弦型函数可以描述股票价格的波动等，通过实际应用案例，可以更好地理解和掌握正弦型函数。

实例解析

以实际案例为载体，详细解析正弦型函数的应用过程，通过分析振动现象中的正弦型函数应用，让读者了解如何将理论知识应用于实践，通过交流电路分析中的正弦型函数应用案例，让读者了解正弦型函数在工程领域的重要性。

本文专题研究了正弦型函数的性质、图像特征以及应用，通过深度解析，使读者对正弦型函数有了更深入的理解，通过实际应用案例的解析，展示了正弦型函数在实践中的应用价值，展望未来，正弦型函数将在更多领域得到应用，如数据分析、机器学习等。

学习建议

为了更好地学习和掌握正弦型函数，读者可以采取以下建议：

1、掌握基础知识：首先要掌握正弦型函数的基本性质、图像特征等基础知识。

2、实践应用：通过实际应用案例，将理论知识应用于实践，加深对正弦型函数的理解。

3、自主学习：除了课堂学习外，读者还可以通过阅读相关书籍、参加在线课程等方式，自主学习正弦型函数的相关知识。

4、勤于思考：在学习过程中，要勤于思考，善于发现问题和解决问题。

本文通过专题研究，全面解析了正弦型函数的性质、图像特征以及应用，希望读者通过本文的学习，能够更好地理解和掌握正弦型函数，并在实践中应用所学知识。